De schaal van Richter

Maart 2011: een van de zwaarste aardbevingen ooit veroorzaakt langs de oostkust van Japan een desastreuze tsunami en een kritieke situatie bij de kerncentrale van Fukushima. Veel slachtoffers en problemen. Dus een zware aardbeving? Zeker, maar niet een-op-een. In de berichtgeving kwam weer regelmatig ‘9.0 op de schaal van Richter’ voorbij. Dat bestaat niet. Hoe stellen we ook al weer de zwaarte van een aardbeving vast? En waarom is de schaal van Richter daarvoor niet altijd de goede maat?

Even terug naar de tijd vóór er uitgebreide seismologische netwerken waren om aardbevingen te meten. We konden altijd wel vaststellen hoeveel mensen de beving hadden gevoeld, hoe groot het gebied was waarin de beving werd waargenomen en hoeveel schade er was. De traditionele indeling in zwaarte is dan ook gebaseerd op de gevolgen die we ervan merkten: de schaal van Mercalli (figuur 1). Door veel mensen over een groot gebied gevoeld, met veel schade? Een zware aardbeving volgens deze aanpak.

Niet natuurkundig

Maar de schade is niet alleen afhankelijk van hoe heftig de grond beweegt. Ook de lokale sociaaleconomische omstandigheden hebben daarop een flinke invloed. Dat blijkt uit twee zeer vergelijkbare aardbevingen, langs een zelfde soort breuk (transform), ongeveer even ondiep (op 10 km), die de bodem op vergelijkbare manier hebben laten bewegen (magnitude 7.1).

De eerste vindt plaats in Haïti, januari 2010. Hele wijken van de hoofdstad Port-au-Prince liggen tegen de vlakte. Huizen van los gestapelde betonnen platen zijn als kaartenhuizen in elkaar gezakt, zeker op de heuvels in de buitenwijken. Hoeveel doden er precies zijn weet niemand, omdat cijfers over het aantal inwoners simpelweg ontbreken. De slecht functionerende overheid is het er wel over eens dat de ramp nét zo heftig is als de tsunami bij Sumatra in 2004 en schat het aantal slachtoffers ‘dus’ op 230.000 (inderdaad, precies zo veel als er door de tsunami omkwamen). Anderhalf miljoen eilanders raken dakloos.

Vergelijk de situatie in Haïti nu eens met die in Nieuw-Zeeland, september 2010. Nabij Darfield, een dorp in de vlakten ten zuiden van Christchurch, vindt ook een aardbeving plaats (niet te verwarren met die in februari 2011, dichter bij de binnenstad). Van rond het moment van de beving is bekend dat er iemand aan een hartstilstand is overleden. Dat zou door de aardbeving kúnnen zijn veroorzaakt. Samen met een aap, bedolven door een ingestort verblijf in een dierentuintje, de enige slachtoffers. Er is beperkte schade aan wegen, spoorweg, heggen, akkerland en enkele boerderijen.

Kortom: de omvang van de schade hangt sterk af van de kwaliteit van de infrastructuur. San Francisco en Japan zijn terdege voorbereid op flinke aardbevingen. Gebouwen worden op ingenieuze manier geconstrueerd. Door de aardbeving zélf, voor de kust van Sendai/Japan in 2011, vielen dan ook geen slachtoffers. Het was de vloedgolf die erop volgde, die de problemen veroorzaakte: duizenden doden, huizen verwoest en zware problemen met de kerncentrale in Fukushima.

Behalve infrastructuur speelt ook de manier waarop de overheid en bedrijven omgaan met seismische dreiging een grote rol. ‘Corruption kills’, schrijven de Engelse seismologen Nicholas Ambraseys en Roger Bilham in 2011 in een artikel in Nature over aardbevingen, slachtofferaantallen, overheidsreguleringen en andere sociaaleconomische factoren. Haïti is hier opnieuw illustratief: een zwakke corrupte overheid, arme bevolking, slechte bouwvoorschriften.

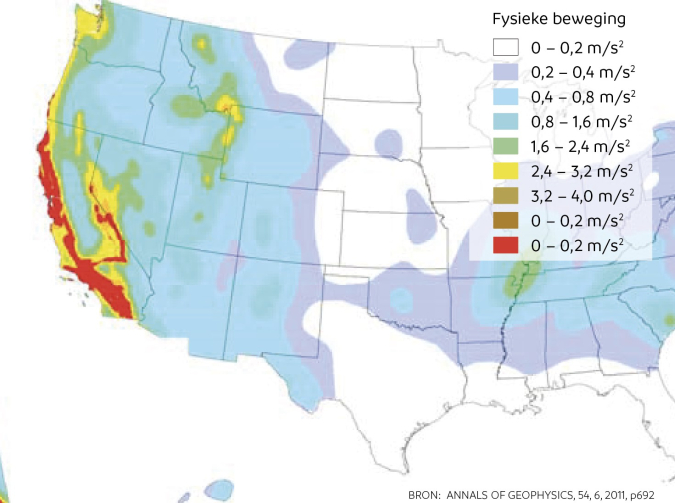
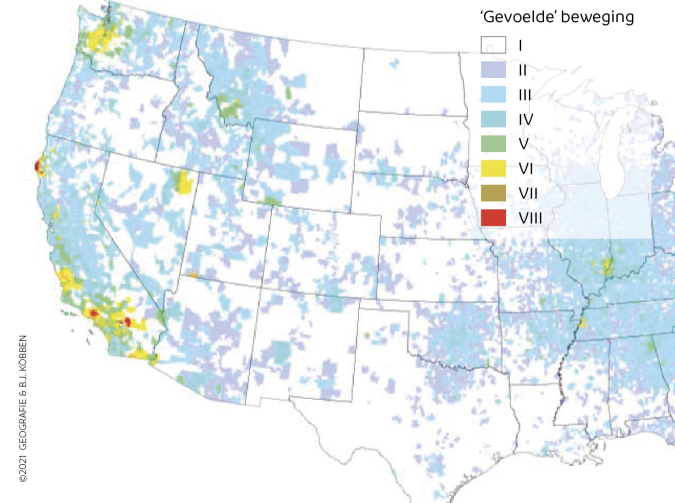
De schaal van Mercalli is zeker handig om de lokale gevolgen en schade in beeld te krijgen: mensen kunnen na een aardbeving meteen meldingen doorgeven, zodat de omvang van de schade snel bekend is en de hulpvraag in te schatten is. Maar deze schaal heeft geen directe natuurkundige relatie met de beving zelf. Stel, er is een aardbeving op de Zuidpool waarbij 3000 pinguïns omvallen. Die is 0 op de schaal van Mercalli. Een ander lastig aspect is dat afhankelijk van hoe vér je van de aardbeving bent, dezelfde beving een ander getal krijgt. Zo is het appels met peren vergelijken als je wilt weten of de aardbeving in jouw land zwaarder was dan die in een ander land. Of als je wilt begrijpen wat er bij een aardbeving nou eigenlijk gebeurt.

Schaal van Richter

Met dat in het achterhoofd plaatste Charles Richter in 1931 een serie seismometers in California, honderden kilometers uit elkaar. Hij wilde meten hoeveel beweging van de grond de apparaten zouden registreren bij een en dezelfde aardbeving op verschillende afstanden van de beving. Vergelijk een aardbeving met een steen die je in het water gooit: waar de steen in het water plonst, ontstaat er een flinke golf, die zich in alle richtingen over het wateroppervlak beweegt. De golf wordt daarbij steeds minder hoog, omdat de energie over een steeds grotere cirkel verdeeld is. Als je de rimpelingen van het water op een bepaalde afstand meet, kun je zeggen hoe hoog de beginplons is, bedacht Richter. En toen was het wachten. En ja hoor. Tot 1932 beleefde Californië enkele lichte aardbevingen. Hoopvol zette Richter de beweging die de meters registreerden uit in een grafiek (figuur 3). De grafiek toont een aantal aardbevingen, waarbij (a) de meeste grondbeweging veroorzaakte. Dicht bij de aardbevingen ging de aarde redelijk op en neer, verder weg nam de beweging heel snel af. Denk aan de steen die in het water plonst, maar anders dan in water verspreidt de golf zich nu ook de diepte in en neemt daardoor nóg sneller af in hoogte!

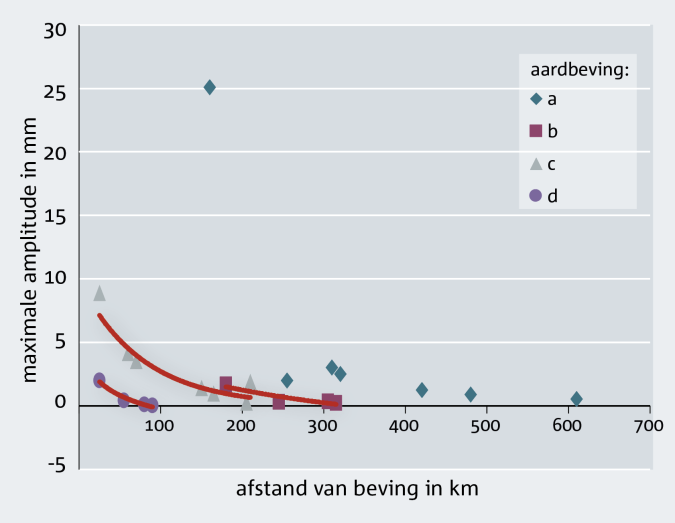
Richter merkte al snel dat het beperkte netwerk van seismografen op een paar honderd kilometer afstand van de aardbeving maar heel kleine verschillen tussen de bevingen kon waarnemen. Zie in figuur 3 het cluster van b, c en a rond de 170-300 kilometer afstand. Daarom zette hij de metingen ook uit in een logaritmische grafiek (figuur 4), dus met stappen van x10 (1, 10, 100, 1000, enzovoort) in plaats van +10 (0, 10, 20, 30). Zo was het verschil duidelijker te zien: vergelijk figuur 3 en 4 maar met elkaar.

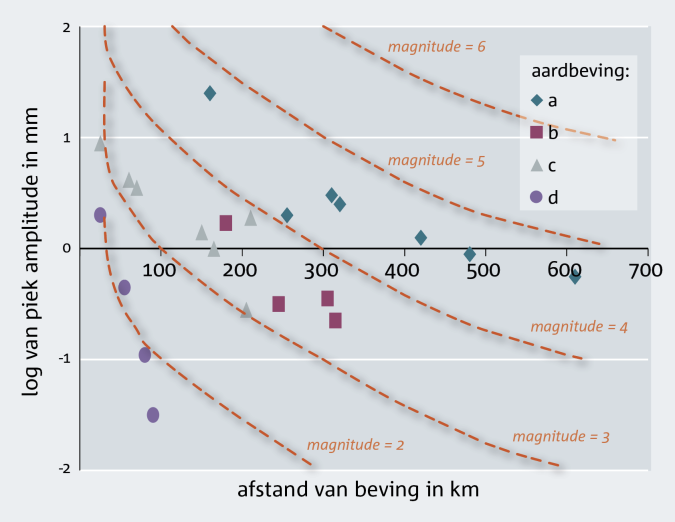
Met zijn beperkte meetnet en meetgegevens kon Richter niet anders dan een willekeurige standaard kiezen. Een gemiddelde aardbeving uit zijn serie die op 100 kilometer afstand maximaal 1 mm beweging veroorzaakte, gaf hij een magnitude 3. Een magnitude 4 aardbeving geeft dan op 100 km afstand een uitslag van 1x10 mm (10 tot de macht 1), een beving van magnitude 2 nog maar 0,1 mm. Waren er in Richters meetperiode in Californië zwaardere bevingen geweest, of juist alleen heel lichte, dan had de schaal van Richter er heel anders uitgezien.

Sleutelen

Tegenwoordig kunnen we met een heel fijn netwerk van meetapparatuur (denk aan Groningen) heel dicht bij een lichte aardbeving een heel kleine beweging vaststellen. Dan heb je het misschien over 0,01 mm beweging op 10 kilometer afstand en kom je in de uiterste linkeronderhoek van de grafiek uit. Een aardbeving van 0 bestáát dus en betekent niet hetzelfde als geen aardbeving.

Goed om je te beseffen: aan het aardoppervlak pal boven een aardbeving van 3.2 op 3 km diepte (hypocentrum), is de diepte meteen de afstand tot de beving. Dat veroorzaakt in het epicentrum, bijvoorbeeld Loppersum, best wat beweging. Maar op 50 km, in de stad Groningen, al nauwelijks meer. En in Den Haag op het Binnenhof al helemaal niet meer.

Daarentegen kan een diepe aardbeving (op honderden kilometers onder het aardoppervlak, veelal in duikende platen) volgens de schaal van Richter behoorlijk zwaar zijn en over een groot gebied wél merkbare trillingen veroorzaken (bijvoorbeeld heen en weer schuddende wolkenkrabbers in Tokio, op 370 km van het epicentrum in Sendai), maar toch weinig schade veroorzaken.

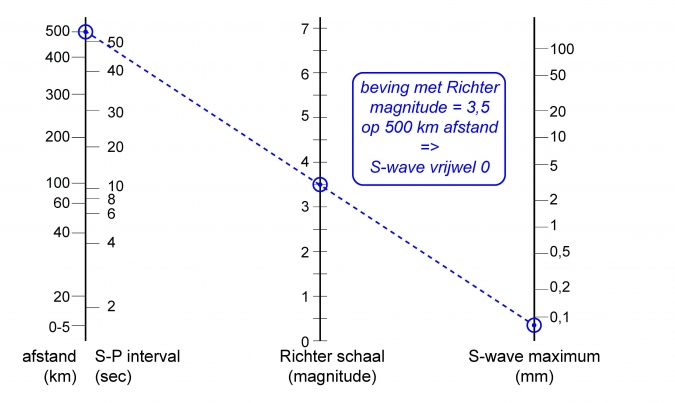
Lichte aardbevingen zijn op grote afstand (> 500 km) niet te meten met de oorspronkelijke schaal van Richter, en ook zware aardbevingen vallen buiten de boot. Je kunt je leerlingen dit zelf laten ontdekken met de opdracht onderaan deze pagina. Daarbij is de ondergrond van Californië niet die van Groningen, dus de schaal is eigenlijk alleen lokaal te gebruiken. Daarom wordt de zwaarte van de aardbeving, de magnitude bij de schaal van Richter, tegenwoordig aangegeven als ML met de L van local.

Richter merkte met zijn leerling Gutenberg zelf al dat de schaal niet goed toepasbaar was bij aardbevingen verder weg. Daarom sloegen ze aan het rekenen met het volledige patroon aan seismische golven van aardbevingen ver weg om daarvan de magnitude te bepalen. Daarvoor stelden ze formules op die ze in overeenstemming brachten met de lokale schaal van Richter. Al die manieren bleken voor- en nadelen te hebben. De ene leverde snel een resultaat, maar was niet precies. De andere was wel precies, maar pas na lange tijd vast te stellen, of niet goed voor diepere aardbevingen.

Andere manier van denken

Inmiddels is ook duidelijk dat de zware bevingen niet per se nóg harder schudden veroorzaken en dat de zwaarte vooral afhangt van hoeveel tijd een breuk blijft schuiven. In Japan in 2011 duurde dat bijvoorbeeld drie volle minuten. Daarom zijn er ook zo veel filmpjes van. Iedereen had genoeg tijd om zichzelf eerst in veiligheid te brengen en daarna nog met een camera aan de slag te gaan. Kortom: er kwam een andere manier van denken in beeld. In plaats van de beweging van de bodem bij een beving te meten, kun je ook bedenken: een aardbeving is het gevolg van verschuiving langs een breukvlak. De beweging langs dat breukvlak houdt ergens ook weer op. Over een lange afstand een grote verschuiving? Zware aardbeving.

Moment magnitude

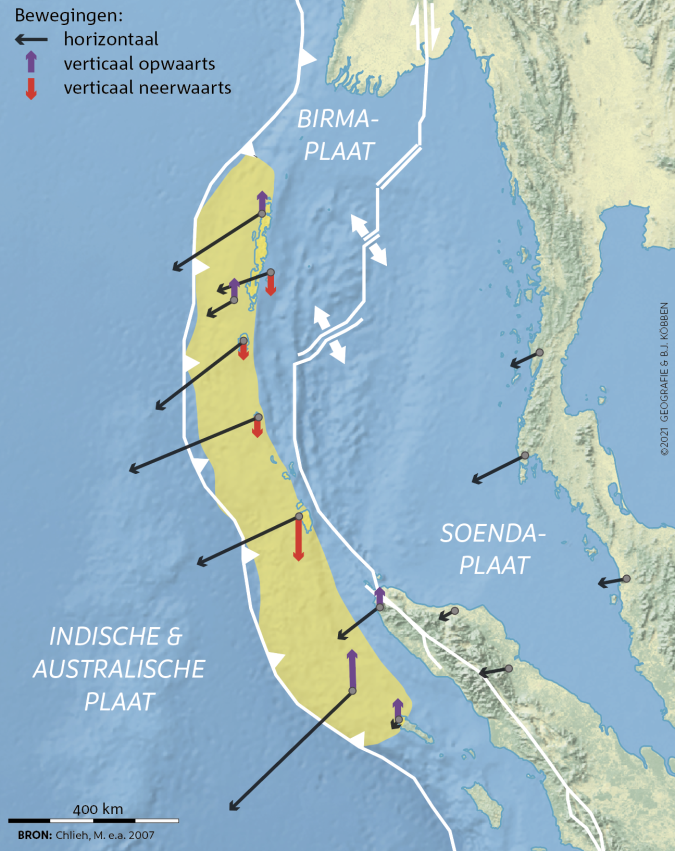
Hoeveel energie is er nodig om een breukoppervlak van x m2 over een gemiddelde afstand van x m te verplaatsen? Vermenigvuldig deze met elkaar en voeg dan nog iets van materiaaleigenschappen van gesteente en/of het breukoppervlak toe. Dat bepaalt hoeveel schuifspanning er nodig is voor hoeveel schuifbeweging. Bij natuurkunde noemen ze zoiets ‘moment’ of ‘arbeid’. Seismisch moment dus, Mo. Tegenwoordig is met gps, satellieten, naschokken en metingen in het veld prima vast te stellen hoeveel verschuiving er is opgetreden. Zo weten we dat bij de aardbeving bij Sumatra in 2004 een stuk plaatgrens van meer dan 1500 x 100 km (gele gebied in figuur 5), dat is alles wat je tot aan de horizon ziet als je van hier naar Barcelona rijdt, gemiddeld een aantal meters verschoof.

Op dezelfde manier kun je ook voor breukbewegingen uit het verleden (bijvoorbeeld van de Peelrandbreuk) in het veld vaststellen hoeveel verschuiving er per keer heeft plaatsgevonden. Dus weten we achteraf hoe zwaar aardbevingen kunnen zijn geweest tot 100 duizenden jaren geleden.

Misschien was het je nog niet opgevallen: uit het rekensommetje van seismisch moment komt geen logaritmische relatie. En hoe kun je dat dan vergelijken met de schaal van Richter? Het zou wat zijn om alle oude gegevens niet meer te kunnen gebruiken. Of alles te moeten omrekenen, voor zover dat al zou kunnen. Dus werd een formule opgetuigd om te zorgen dat de moment magnitude (Mw, met de ‘w’ van work) voor het deel waarin Richters schaal prima werkt (ongeveer magnitude 3 tot 5.5) gelijk is aan de schaal van Richter op basis van het seismische moment: Mw = 2/3logMo - 10.7. Inderdaad, een ingewikkelde formule, maar op die manier gebruiken we via een achterdeur nog altijd de schaal van Richter.

Bij zwaardere aardbevingen gaan ML en Mw steeds verder uit elkaar lopen, Richters schaal onderschat die. Dus bij aardbevingen boven 5.5 kun je niet meer spreken van ‘op de schaal van Richter’. Ook al doen de NOS en de Volkskrant dat gewoontegetrouw nog wel. En als docent deed jij dat misschien ook nog. Nu weet je waarom je een ‘aardbeving met magnitude 8.2’ hoort te zeggen. En je leerlingen straks ook.

Opdracht: meet de kracht op de schaal van Richter

Hoe kun je aan de hand van de gemeten grondbeweging en de afstand tot de beving bepalen welke kracht een aardbeving op de schaal van Richter heeft?

Het begint ermee dat je de afstand tussen seismograaf en aardbeving moet bepalen. Die is redelijk makkelijk te reconstrueren: een aardbeving veroorzaakt verschillende soorten seismische golven, die niet allemaal dezelfde snelheid hebben en een kenmerkend patroon veroorzaken op een seismogram. De ene (P-wave, van Primary of Pressure) is sneller dan de andere (S-wave, Secondary of Shear). Het verschil in snelheid maakt dat hoe verder je van de aardbeving verwijderd bent, des te meer voorsprong de P-wave heeft op de S-wave. Vergelijk het met bliksem en donder: door het verschil in aankomst tussen beide te tellen, kun je bepalen hoe ver het onweer nog van je vandaan is. Drie tellen is ongeveer 1 kilometer (licht gaat ‘oneindig snel’, geluid met ongeveer 300 m per seconde. Dus na 3 seconden heeft het licht een voorsprong van 3 sec. x 300 m/sec = 900 m).

Bij een aardbeving heb je de volgende gegevens nodig: de snelheid van de P-wave (Vp), de snelheid van de S-wave (Vs) en de tijd (t) die zit tussen de aankomst van beide golven bij de seismograaf. De formule luidt Vp * Vs/(Vp-Vs) * t. Samen met de maximale uitslag (piekamplitude) van de S-wave kun je dan ook de magnitude op de schaal van Richter bepalen. Laten we dat eens doen.

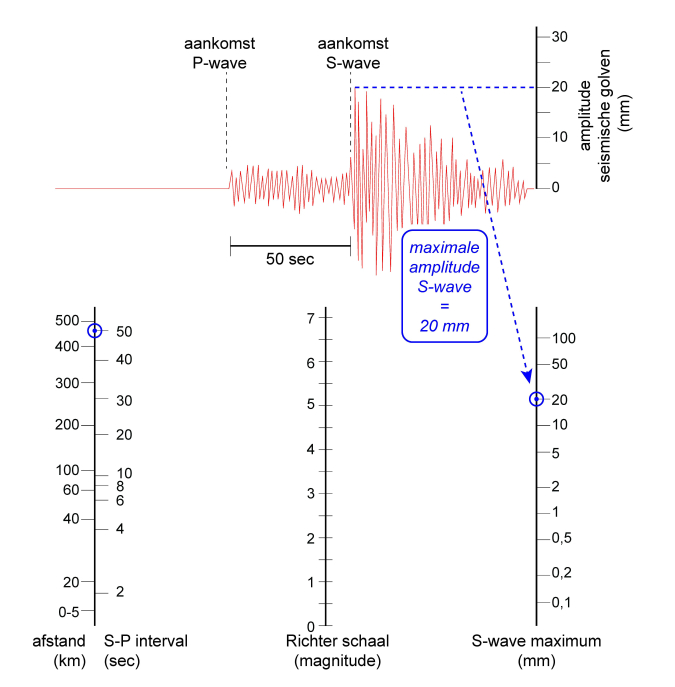
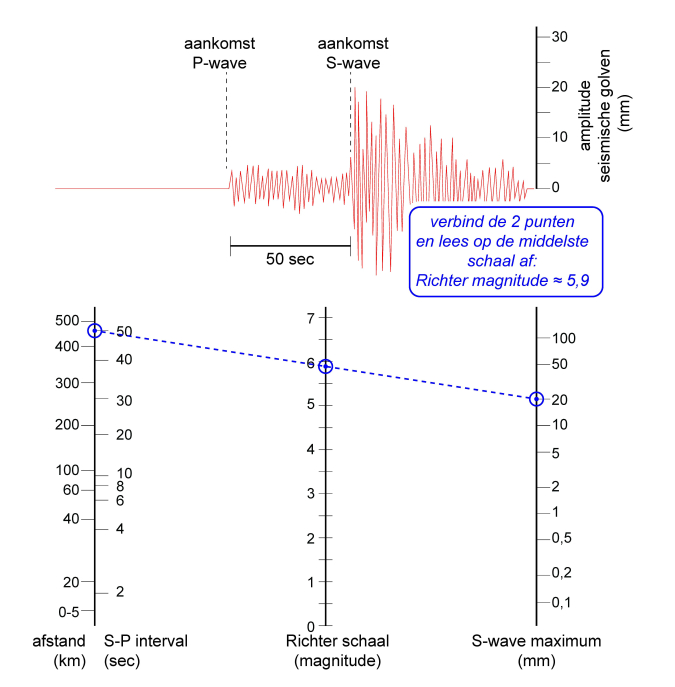
En nu een aardbeving van 3.5 in Parijs (zo’n 500 kilometer verderop), zie de tekening hieronder. En een aardbeving van 7.0 in Limburg (voor de meesten van ons 200 kilometer verderop). Wat zou je dan aan grondbeweging moeten krijgen? Let op dat de balken links en rechts ook logaritmisch zijn. Is de uitkomst dan nog meetbaar of realistisch?

BRONNEN:

• Ambraseys, N., & Bilham, R. (2011). Corruption kills. Nature, 469, 153-155.
• Chlieh M., et al. (2007). Coseismic slip and afterslip of the great (M W9.15) Sumatra-Andaman earthquake of 2004. Bulletin of the Seismological Society of America 97: 152-173.
• Richter, C.F. (1935). An instrumental earthquake magnitude scale. Bulletin of the Seismological Society of America, 25, 1-32.
• Subarya, C. et al. (2006). Plate-boundary deformation associated with the great Sumatra-Andaman earthquake. Nature, 440: 46-51.
• Universiteit van Nederland, 23 september 2021. Moet de schaal van Richter in de prullenbak?
• NOSop3. Tikkende tijdbom: de volgende mega-aardbeving