Buys Ballot op een A4tje

De wet van Buys Ballot is misschien wel een van de taaiste onderwerpen bij aardrijkskunde. De oplossing: laat de globe staan en teken één halfrond van bovenaf op een A4tje.
Willem Sanders (De Nieuwe School) wil de wet van Buys Ballot illustreren, maar loopt er tegenaan dat zijn aanpak maar één kant op werkt. ‘Als ik op een draaiende globe vanaf 30° graden NB en ZB richting de evenaar beweeg, lukt dit volgens de Wet van Buys Ballot, maar als we vervolgens dezelfde methode toepassen vanaf 30° NB en ZB richting 60° NB en ZB, zien we de afwijking van de wind juist verkeerd om. Is er een betere methode?’
Roterende bol
De afwijking die een luchtstroom krijgt als die over de aarde beweegt, is voor veel leerlingen een van de lastigste onderwerpen in de schoolaardrijkskunde. Wellicht heeft het ermee te maken dat je dit onderwerp niet goed kunt begrijpen zonder de aarde als een roterende bol te zien. Het probleem wordt nog een beetje verergerd doordat de situatie meestal van ‘opzij’ wordt getoond: de evenaar in het midden en de luchtstromen op het noordelijk en zuidelijk halfrond. Op die manier krijg je per definitie geen overzicht van de beweging van de lucht wanneer de aarde een hele rotatie doorloopt en moet je dus de helft van de beweging zelf invullen. Veel te lastig.
Eén halfrond
Om het handiger aan te pakken, moet je de situatie versimpelen: kijk gewoon naar één halfrond. Immers, op dat ene halfrond is de beweging overal hetzelfde. Laten we het noordelijk halfrond nemen. Daar zie je de aarde linksom draaien (tegen de klok in). De bolling kun je even wegdenken, beschouw het noordelijk halfrond gewoon als een platte schijf, van bovenaf gezien. Het middelpunt is de noordpool, dus elke pijl die je op deze schijf tekent die naar het midden wijst is een pijl naar het noorden. Elke pijl die naar de rand wijst is een pijl naar het zuiden. Elke pijl parallel aan een breedtecirkel met de klok mee wijst naar het westen en elke pijl parallel aan een breedtecirkel tegen de klok in wijst naar het oosten.
Vaste aarde
Al deze richtingen (noord, zuid, oost en west) hebben alleen betekenis op de aarde. Er is niets bijzonders aan de kompasrichtingen als je naar het wijdere universum kijkt, waar de aarde doorheen draait. In dat wijdere universum geldt de eerste wet van Newton, oftewel het principe van de traagheid (inertie). Een bewegend voorwerp blijft bewegen in dezelfde richting en met dezelfde snelheid, tenzij er een kracht op wordt uitgeoefend. Anders gezegd voor onze context van een draaiende planeet: dingen gaan rechtdoor, tenzij ‘iets’ ze de bocht om duwt. Lucht die op aarde beweegt, heeft de neiging om in ‘universele’ zin rechtdoor te gaan. De vaste aarde draait echter ‘opzij’. In de vaste aarde zit alles stevig aan elkaar, dus die beweegt als één geheel, Maar de atmosfeer zit een stuk losser aan de vaste aarde gekoppeld en bewegende lucht gaat daarom niet perfect mee met de draaiing. De lucht gaat (een beetje) ‘rechtdoor’, terwijl de aarde ‘linksaf’ gaat (als je op het noordelijk halfrond kijkt). Ons referentiekader is de vaste aarde. Wij zien dus niet de aarde ‘linksaf’ gaan, maar juist de lucht rechtsaf. En dat is het Coriolis-effect oftewel de wet van Buys Ballot.
In beeld
Hoe kun je dit nou illustreren? Neem de schijf van hierboven (bijvoorbeeld een cirkel die je op een stuk papier tekent). Idealiter teken je in de cirkel de noordpool en de breedtecirkels van 30° en 60°; de omtrek van de cirkel is de evenaar (figuur 1). Zet ergens een stip, bijvoorbeeld ergens op de 30°-cirkel (noem het de Azoren) en teken een klein stukje pijl richting de noordpool. Onthoud de ‘universele’ richting van die pijl, teken hem bijvoorbeeld parallel aan de tafelrand of iets anders dat in dezelfde oriëntatie blijft. Roteer nu de schijf een beetje linksom, zeg 45° (drie uur draaien van de aarde). De lucht wil ‘rechtdoor’, dus teken het volgende stukje pijl opnieuw in de oorspronkelijke richting. Omdat de aarde gedraaid is, loopt de pijl dus niet meer richting het noorden, maar naar het noordoosten. Herhaal dit procedé en het volgende stukje beweging is in oostelijke richting, enzovoorts. Er ontstaat een serie pijltjes die een rechtsaf buigende luchtstroom voorstellen. Dit is vergelijkbaar met de draaiing rondom en weg van een hogedrukgebied op het noordelijk halfrond, zoals het Azorenhoog. Exact dezelfde stappen kun je herhalen op elke plek van de schijf met een beginbeweging in elke richting met steeds dezelfde uitkomst.
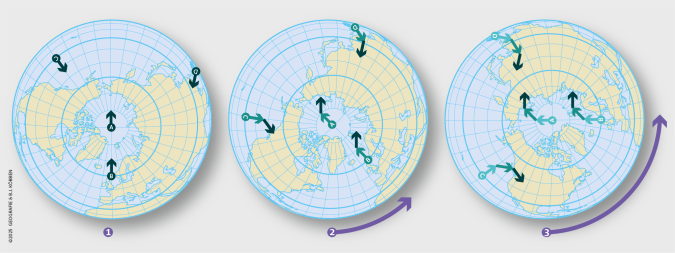
Om de situatie op het zuidelijk halfrond te illustreren draai je de schijf rechtsom, met als resultaat pijlen die naar links afbuigen. Bedenk dat de platte schijf slechts een benadering is: in werkelijkheid is het Coriolis-effect het sterkst op de pool en afwezig op de evenaar. De beste manier die deze geoloog kent om het effect op de luchtstromen te illustreren is middels de Nullschool Earth-animatie (https://earth.nullschool.net/). Deze virtuele globe geeft de luchtstromen weer en kun je kantelen, zodat je alleen op één halfrond kijkt. Het is dan goed te zien dat alle hogedrukgebieden op dezelfde manier draaien (met de klok mee) en dat die draaiing precies tegengesteld is aan de draaiing van de aarde (tegen de klok in).
